RF Design - Power

This post is dedicated to RF Power theory. In today's busy world Power is consumed by various smart devices such as PC's and smartphones. Whether you connect your Phone to a cellular tower or your PC to your Wi-Fi router, the Power plays a huge role in designing Radio Frequency or Microwave AC circuits.

Power in RF Design:

• Avoid loss
• Maximum Power transfer

Instantaneos Power:

• p(t) = v(t).i(t)   OR   v(t)² / R

• Imagine having a simple closed circuit with voltage source and a resistor connected. Then the instantaneous power is the power at a specific time. For example, v(t=100) = 2 v, and R = 50 ohm. Then, p(t=100) = v(100)² / R = 2² / 50 = 4 / 50 W.

Average Power:

average v(t)² over time

• Pavg = 1 / T ∫0T.​ . p(t) dt = (1 / R) . (1 / T) ∫0Tv(t)² 

• Usually, we deal with periodic waveforms. Hence, T is used as a time period of the periodic waveform. 

• The average v(t)² over time = < V(t)² > =  (1 / T) ∫0Tv(t)² 

RMS voltage

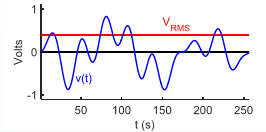
• Vrms =  √< V(t)² >  =  root mean square or RMS voltage.

• Thus, the average power dissipated in the resistor R is P = < V(t)² > / R  or  V²rms / R.

• Example Problem: RMS value? of V(t) = 2cos(wt) [voltage source], and average power dissipated in 50 ohm resistance?
• Pavg = 1 / T ∫0T.​ . p(t) dt = (1 / R) . (1 / T) ∫0Tv(t)² 

                since, V(t) = A cos (wt) => < V(t)² > =  (1 / T) ∫0Tv(t)²

• (1 / T) ∫₀^T   A² cos²(wt) =(since avg. of cos from 0 to T = 0 [zero] ) 
• => < V² (t) > = A² / 2
• Pavg = 1/R . A² / 2 = 1 / 50 . 4 / 2 = 2 / 50

• Vrms =  √< V(t)² >  = A / √2 = 2 / √2

Power and Phasor:

• 2sin(wt) = 2cos(wt - 90)
• Same Phase
• e^-j90 = sin (wt) = cos (wt -90) = I, current
• Z = R; I = V / Z = | V | e^-j90  / R e^j0 

• Z = jLw; I =V / Z = | V | e^j0 / ( Lw )e^j90  = (| V | / Lw)e^-j90

• Pure imaginary phase difference of 90
• 90 deg phase difference between I and V
• Z = jLw = ( Lw )e^j90

Power

• p(t) = v(t) i(t) = |V| |I| cos (wt + θv)  cos (wt + θ1) = ( |V| |I| ) / 2 . {cos (2wt + θv + θ1) + cos(θv - θ1)}, where yellow highlighted part of the equation is = 0 mathematically.

• Average power: Pavg = ( |V |  | I | )/2 . cos (θv - θ1), where ϕ = θv - θ1

• Pavg = ( |V |  | I | )/2 . cos ϕ

• Vrms = | V | / √2;  Irms = | I | / √2 

• Thus, Pavg = Vrms Irms cos(θv - θ1)

• Example, Pavg = ( |V |  | I | )/2 . cos (θv - θ1) = 0, since (θv - θ1) = 90deg.

*Advanced concepts on power to be covered in another post.